[코드트리 챌린지] 8주차 - 동적계획법(DP)3

사실 휴가가기전에 7주차를 쓰려고 빡세게 1000점이나 채웠는데

비행기 타러가다가 까먹고 호로록 날려버린 건 비밀 ㅎㅎ

 

동적계획법이 생각보다 유형이 되게 많고👀

이 동적계획법을 꿰뚫는 skeleton code가 있는 것도 아니기 때문에

직접 하나하나 해봐야 해서 굉장히 시간을 많이 썼다😢

 

코드트리에서는 동적계획법 세션에서 기본개념 1문제 - 심화문제 1문제를 세트로 주는데

심화문제가 기본개념에 비해 굉장히..어...어려워요 ㅠㅠㅠㅠ

 

무튼 제일 기억에 남는 문제는 

릴레이 문제라서 링크 공유가 되지 않네용 ㅠㅠ

이전 주의 챌린지 보상을 받지 못해서 열심히 푼 다른 DP 문제들의 제출 코드를 볼 수 없었다...

(아니 근데 제가 제출한 코드도 못보게 하는 건 너무하다구 생각합니다 !!!!!!)

 

이 문제는 만약 주어진 수열이 3-7-5-2-6-1-4라면 다음과 같이 최소 4번의 과정만 거치면 오름차순으로 만들 수 있기 때문에 "4"라는 답을 출력하면 되는 문제이다.

초기 상태          : 3 7 5 2 6 1 4
2를 맨 앞으로 이동 : 2 3 7 5 6 1 4
7을 맨 뒤로 이동   : 2 3 5 6 1 4 7
1을 맨 앞으로 이동 : 1 2 3 5 6 4 7
4를 5 앞으로 이동  : 1 2 3 4 5 6 7

 

굉장히 오래 고민했는데 문제에서 찾아야 하는 핵심✨은 크게 2가지이다.

 

Sol 1

1부터 n까지의 숫자가 모두 빠짐없이 나온다! 즉 오름차순 수열을 만들려고 할 때 1-3-4와 같이 특정 숫자가 빠지는 일이 절대 일어나지 않는다. 무조건 1-2-3-4-5의 순으로 수열이 완성된다. 더 쉽게 말하자면 특정 숫자(1)는 무조건 놓여져야 하는 정답 위치(첫번째, 2의 앞에)가 있는 것이다.

 

Sol 2

최장증가부분수열(LIS) 알고리즘을 활용하자! Sol1 때문에 주어진 수열에서 최장 증가 부분 수열을 찾는다면 해당 부분 수열은 움직일 필요 없이 나머지 숫자들만 제자리, 정답 위치에 가져다 놓으면 조건에 맞는 수열이 완성되는 것이다.

 

따라서 최장 증가 부분 수열에 속하지 않은 다른 숫자들만 움직이면 되므로 답안은 다음과 같다.

n = int(input())
number = [int(input()) for _ in range(n)]
dp = [1] * n

for i in range(n) :
    for j in range(i) :
        if number[j] < number[i] :
            dp[i] = max(dp[j]+1, dp[i])

print(n-max(dp))

 

다 풀고 너무 허탈해서 빠직💢했지만, 오래 고민한만큼 절대 까먹지는 않을 듯 싶다 ㅎㅎ

Code 답 자체는 굉장히 쉬운데 이런 idea가 어려운지 티어도 골드5였다 후훗

정말 이거 풀고 아자뵤!를 외침 ㅎㅎ

아무튼 dp를 아주 죽어라 파보았더니!!

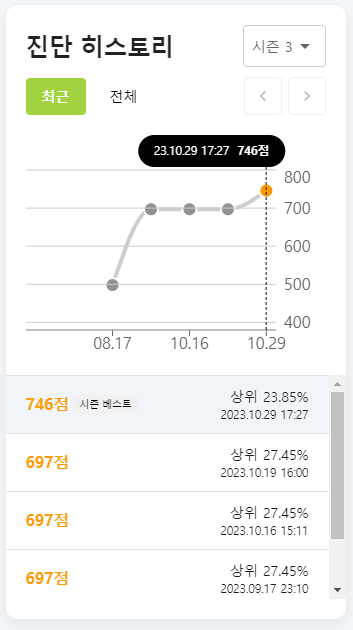
드디어 올랐다 나의 실력진단 점수 ㅠㅠㅠㅠㅠㅠ 부족한 부분도 dp가 아니라 자료구조 응용부분이라고 나왔다

공부하면 뚫리긴 하는구나..라고 느낌!

 

다음주에 보상을 주시면 더 열심히 해보겠습니다 ㅎㅎㅎㅎ

 

제발 코드트리 블챌 시즌2도 주세요... 이번에는 상품 받을래.... 젭알..